Summary
বর্তমান যুগ তথ্যপ্রযুক্তির যুগ হিসেবে চিহ্নিত হলেও, তথ্য এবং উপাত্ত ব্যবহার করে সিদ্ধান্ত নেয়া শেখা অত্যন্ত গুরুত্বপূর্ণ।
এই অধ্যায়ে তথ্য ও উপাত্তের পাশাপাশি এসব থেকে সিদ্ধান্ত নিতে ব্যবহৃত বিভিন্ন পদ্ধতি নিয়ে আলোচনা করা হয়েছে। তথ্য ও উপাত্তের সঠিক ব্যবহার সম্পর্কে ধারণা লাভের মাধ্যমে বাস্তব সমস্যার সমাধান করা সহজ হবে।
অধ্যায় শেষে শিক্ষার্থীরা:
- তথ্য ও উপাত্ত কী তা ব্যাখ্যা করতে পারবে।
- এবং অবিন্যস্ত উপাত্তের গড়, মধ্যক ও প্রচুরক নির্ণয় করতে পারবে।
- রেখাচিত্র অঙ্কন এবং বর্ণনা করতে পারবে।
আমরা যে পৃথিবীতে বসবাস করছি তা অসংখ্য তথ্য এবং উপাত্তে ভরপুর। তাই বর্তমান সময়কে তথ্যপ্রযুক্তির যুগ বলা হয়। তথ্যপ্রযুক্তির যুগে বাস করে কিভাবে তথ্যকে ব্যবহার করতে হয় এবং তথ্য ও উপাত্ত থেকে কিভাবে সিদ্ধান্ত নিতে হয় তা জানা প্রত্যেক মানুষের জন্য গুরুত্বপূর্ণ এবং অপরিহার্য। এ সকল দিক বিবেচনা করে এই অধ্যায়ে তথ্য, উপাত্ত এবং উপাত্তকে সাজিয়ে তা থেকে গুরুত্বপূর্ণ সিদ্ধান্ত নেয়ার জন্য ব্যবহৃত বিভিন্ন পদ্ধতি নিয়ে আলোচনা করা হয়েছে। একই সাথে কিভাবে তথ্য ও উপাত্তকে ব্যবহার করতে হয় সেই সেই দিক নিয়েও আলোচনা করা হয়েছে। এই অধ্যায়ের আলোচিত বিষয়গুলো সম্পর্কে সঠিকভাবে ধারণা লাভ করতে পারলে অনেক বাস্তব সমস্যার সমাধান করা সহজ হয়ে যাবে।
অধ্যায় শেষে শিক্ষার্থীরা -
- তথ্য ও উপাত্ত কী তা ব্যাখ্যা করতে পারবে।
- শ্রেণি ব্যবধান না করে অবিন্যস্ত উপাত্তের গড়, মধ্যক ও প্রচুরক নির্ণয় করতে পারবে।
- রেখাচিত্র অঙ্কন করতে পারবে।
- অঙ্কিত রেখাচিত্র বর্ণনা করতে পারবে।
# বহুনির্বাচনী প্রশ্ন
৬ জন শিক্ষার্থীর ২০ নম্বরের পরীক্ষায় প্রাপ্ত ফলাফল: ৮, ১০, ১৬, ১৪, ১৬, ২০
তথ্যনির্ভর বিশ্বে প্রতিনিয়ত আমরা বিভিন্ন তথ্যের সম্মুখীন হই এবং এর ব্যাপক ব্যবহার দেখতে পাই। প্রতিদিন শিক্ষক অধ্যয়নরত শিক্ষার্থীদের হাজিরা রাখেন। প্রতি পরীক্ষার শেষে শিক্ষার্থীদের প্রাপ্ত নম্বর সংরক্ষণ করেন এবং এর উপর ভিত্তি করে শিক্ষার্থীদের দুর্বলতা চিহ্নিত করেন ও তা দূরীকরণের জন্য প্রয়োজনীয় ব্যবস্থা নেন। এছাড়া আমরা দৈনিক পত্রিকা, রেডিও, টেলিভিশন ইত্যাদি গণমাধ্যম থেকে আবহাওয়া, খেলাধুলা, বাজারদর ইত্যাদি সম্পর্কে বিভিন্ন তথ্য পেয়ে থাকি।
কোনো বিদ্যালয়ের ৬ষ্ঠ শ্রেণির গণিতে ৬০ এর অধিক নম্বর প্রাপ্ত ১০ জন এবং ৬০ এর কম নম্বর প্রাপ্ত ১০ জন শিক্ষার্থীর নম্বর নিচের তালিকায় দেওয়া হলো:

এই তুলনামূলক তালিকা থেকে কম নম্বর প্রাপ্তির কারণ বিশ্লেষণ করে প্রয়োজন অনুযায়ী পদক্ষেপ গ্রহণ করা যায়। সুতরাং বিভিন্ন বিষয় বা ঘটনার সংখ্যাসূচক তথ্য কীভাবে পাওয়া যায় এবং কীভাবে প্রয়োগ করতে হয় সে সম্বন্ধে পরিষ্কার ধারণা থাকা প্রয়োজন।
উপরের তালিকায় যে বেশি নম্বর ও কম নম্বর দেখানো হয়েছে তা হলো সংখ্যাভিত্তিক তথ্য।
উপরের তালিকায় যে দুইটি সংখ্যাসূচক তথ্য দেওয়া হয়েছে তার প্রত্যেকটি এক একটি পরিসংখ্যান অর্থাৎ, ছাত্রদের প্রাপ্ত নম্বর ৯০, ৮০, ৭৫, ৭০ একটি পরিসংখ্যান। অনুরূপভাবে, প্রাপ্ত নম্বর ৫০, ৪৫, ৪০, ৩৫ আর একটি পরিসংখ্যান।
উপাত্ত: পরিসংখ্যানে বর্ণিত সংখ্যাসূচক একটি তথ্য প্রাপ্ত বেশি নম্বরসমূহ। এগুলো হলো পরিসংখ্যানের উপাত্ত। অনুরূপভাবে, কম নম্বর প্রাপ্ত তথ্যও পরিসংখ্যানের উপাত্ত। পরিসংখ্যানে বর্ণিত তথ্যসমূহ যেসকল সংখ্যা দ্বারা প্রকাশ ও উপস্থাপন করা হয়, তা হচ্ছে পরিসংখ্যানের উপাত্ত।
তবে একটি মাত্র সংখ্যা দ্বারা প্রকাশিত উপাত্ত পরিসংখ্যান নয়। যেমন, রনির বয়স ৪৫ বছর, পরিসংখ্যান নয়।
# বহুনির্বাচনী প্রশ্ন
ধরা যাক, কোনো বিদ্যালয়ের ৬ষ্ঠ শ্রেণিতে অধ্যয়নরত ২০ জন শিক্ষার্থীর ওজন (কেজিতে) নিম্নরূপ: ৫০, ৪০, ৪৫, ৪৭, ৫০, ৪২, ৪৪, ৪০, ৫০, ৫৫, ৪৪, ৫৫, ৫০, ৪৫, ৪০, ৪৫, ৪৭, ৫২, ৫৫, ৫৬। এখানে, উপস্থাপিত নম্বরসমূহ অবিন্যস্তভাবে আছে। এই ধরনের উপাত্তসমূহকে অবিন্যস্ত উপাত্ত বলে। এ রকম অবিন্যস্ত উপাত্ত থেকে চাহিদামাফিক সিদ্ধান্ত নেওয়া খুবই কষ্টসাধ্য। কিন্তু উপাত্তসমূহ যদি মানের অধঃক্রমে বা ঊর্ধ্বক্রমে সাজানো যায় তাহলে প্রায়োজনীয় সিদ্ধান্ত সহজে নেওয়া যায়। সংগৃহীত উপাত্তসমূহ মানের ঊর্ধ্বক্রমে সাজালে হবে ৪০, ৪০, ৪০, ৪২, ৪8, 88, ৪৫, ৪৫, ৪৫, ৪৭, ৪৭,৫০, ৫০, ৫০, ৫০, ৫২, ৫৫, ৫৫, ৫৫, ৫৬। এভাবে সাজানো উপাত্তসমূহকে বিন্যস্ত উপাত্ত বলে।
উদাহরণ ১। ৬ষ্ঠ শ্রেণিতে অধ্যয়নরত শিক্ষার্থীর মধ্যে সব থেকে লম্বা ১০ জনের উচ্চতার (সে.মি.তে) পরিসংখ্যান হলো: ১২৫, ১৩৫, ১৩০, ১৩৮, ১৩৭, ১৪২, ১৪৫, ১৫২, ১৫০, ১৪০।
(ক) উপরে বর্ণিত উপাত্তসমূহ বিন্যস্ত কর।
(খ) বর্ণিত উপাত্তসমূহ সারণিভুক্ত কর।
সমাধান: (ক) প্রদত্ত উপাত্তসমূহ মানের ঊর্ধ্বক্রমে বিন্যস্ত করা হলে হবে ১২৫, ১৩০, ১৩৫, ১৩৭, ১৩৮, ১৪০, ১৪২, ১৪৫, ১৫০, ১৫২।
(খ) সারণি
| শিক্ষার্থীর ক্রমিক নং | উচ্চতা (সে.মি.) | শিক্ষার্থীর ক্রমিক নং | উচ্চতা (সে.মি.) |
| ১ | ১২৫ | ৬ | ১৪০ |
| ২ | ১৩০ | ৭ | ১৪২ |
| ৩ | ১৩৫ | ৮ | ১৪৫ |
| ৪ | ১৩৭ | ৯ | ১৫০ |
| ৫ | ১৩৮ | ১০ | ১৫২ |
কাজ: ১। তোমাদের শ্রেণিতে অধ্যয়নরত শিক্ষার্থীদের ২০ জন করে নিয়ে ২/৩টি দল গঠন করে গণিতে প্রাপ্ত নম্বর সংগ্রহ ও বিন্যস্ত কর। |
উদাহরণ ২। কোনো ক্রিকেট দলের ৫ জন বোলারের বল করার পরিসংখ্যান সারণিভুক্ত করে নিচে দেখানো হলো:
| ক্রমিক নং | নাম | ওভার | মেইডেন ওভার | প্রদত্ত রান | উইকেট প্রাপ্তি |
| ১ | সাকিব | ৫ | ১ | ৩৫ | ২ |
| ২ | মাশরাফি | ৫ | ২ | ৩২ | ৩ |
| ৩ | রাজ্জাক | ৪ | ১ | ৪০ | ১ |
| ৪ | আশরাফুল | ৩ | ০ | ৩৫ | ০ |
| ৫ | মনি | ৫ | ৩ | ৩০ | ১ |
| কাজ: ১। ক্রিকেট খেলার দুইটি স্কোর বোর্ডের নিচের তথ্য সারণিভুক্ত কর: (ক) ৫ জন বোলারের নাম, ওভার, মেইডেন ওভার, প্রদত্ত রান, উইকেট প্রাপ্তি। (খ) ৫ জন ব্যাটসম্যানের নাম, রান, বল মোকাবেলা করা, সময়কাল। ২। তোমাদের শ্রেণির যেকোনো ১০ জনের উচ্চতা, ওজন ও গণিতে প্রাপ্ত নম্বরের সংখ্যাভিত্তিক উপাত্ত সংগ্রহ করে বিন্যস্ত কর এবং বিন্যস্ত উপাত্তের সারণিভুক্ত করে দেখাও। |
# বহুনির্বাচনী প্রশ্ন
কোনো পরিবারে বছরে ৪২০ কেজি চাল লাগে। প্রতিমাসে যে একই পরিমাণ চাল লাগে তা নয়। কোনো মাসে বেশি আবার কোনো মাসে কম লাগে। কোন মাসে কতটুকু চাল খরচ হয়েছে তার সঠিক হিসাব জানতে হলে লিখিত হিসাব রাখতে হবে। এটা বেশ বিরক্তিজনক। তাই আমরা প্রতিমাসে গড়ে কতটুকু চাল লাগে তার হিসাব জানতে চাই এবং জিজ্ঞেস করি গড়ে কী পরিমাণ চাল প্রয়োজন হয়? এ প্রশ্নের উত্তরে আমরা খুব সহজেই বলতে পারি, (৪২০ ১২ = ৩৫ কেজি) মাসে গড়ে ৩৫ কেজি চাল লাগে। এখানে আমরা মোট চালের পরিমাণকে বৎসরের মাসের সংখ্যা ১২ দিয়ে ভাগ করে চালের গড় পরিমাণ নির্ণয় করে থাকি। এভাবে আমাদের দৈনন্দিন জীবনে গড়ের ব্যাপক ব্যবহার হয়ে থাকে। যেমন, তোমাদের শ্রেণিতে অধ্যয়নরত সকল শিক্ষার্থী প্রতিদিন স্কুলে আসতে পারে না। উপস্থিতি সংখ্যা কোনো দিন বাড়ে আবার কোনো দিন উপস্থিতির সংখ্যা কমে। তাই আমরা জানতে চাই প্রতিদিন গড়ে কতজন শিক্ষার্থী উপস্থিত হয়? উত্তরে আমরা বলে থাকি, গড়ে ৮০ জন শিক্ষার্থী উপস্থিত হয়।
গড়: সংগৃহীত উপাত্তসমূহের সমষ্টিকে উপাত্তসমূহের সংখ্যা দিয়ে ভাগ করে গড় পাওয়া যায়।

উদাহরণ ৩। ২৫ নম্বরের প্রতিযোগিতামূলক গণিত পরীক্ষায় ১০ জনের প্রাপ্ত নম্বর ২০, ১৬, ২৪, ১৬, ১৬, ২০, ১৫, ১২, ১৬, ১৫। প্রতিযোগীদের প্রাপ্ত নম্বরের গড় নির্ণয় কর।
সমাধান: প্রাপ্ত নম্বরের গড়
বা ১৭
নির্ণেয় গড় নম্বর ১৭
এভাবে আমরা বিভিন্নভাবে বিভিন্ন পরিসংখ্যানের গড় ব্যবহার করে থাকি। যেমন, রিশা পরপর ৫ দিন ৩ ঘণ্টা, ৪ ঘণ্টা, ৫ ঘণ্টা, ২ ঘণ্টা ও ৬ ঘণ্টা করে পড়ে। যদি সেতু তাকে জিজ্ঞেস করে সে দিনে কত ঘণ্টা করে পড়ে? উত্তরে সে তার কোনদিনের পড়ার সময় বলবে? এই ক্ষেত্রে গড়ে সে প্রতিদিন কত ঘণ্টা করে পড়ে সেটা বলা হবে যুক্তিযুক্ত। তাই সে বলবে প্রতিদিন গড়ে ঘণ্টা বা ৪ ঘণ্টা করে পড়ে।
এখানে যে গড় আমরা ব্যবহার করি তা গাণিতিক গড়।
তাই রিশার প্রতিদিন পড়ার গড় ঘণ্টা ঘণ্টা = ৪ ঘণ্টা
অর্থাৎ, পড়ার সময়ের গাণিতিক গড় ৪ ঘণ্টা।
| কাজ: ১। একুশের বইমেলা থেকে তোমাদের শ্রেণির জন্য ১৫টি বই ১৫০০ টাকায় কেনা হয়েছে। প্রতিটি বইয়ের গড় মূল্য কত? ২। তোমাদের শ্রেণির ১০ জন শিক্ষার্থীর উচ্চতার মাপ (সেন্টিমিটারে) ও উচ্চতার গড় নির্ণয় কর। |
# বহুনির্বাচনী প্রশ্ন
গাণিতিক গড় দেখে সংগৃহীত উপাত্তের বৈশিষ্ট্য সম্বন্ধে নেওয়া সিদ্ধান্ত অনেক সময় বাস্তবতার সাথে মিলে না। যেমন, ৫ জন ছাত্রের প্রাপ্ত নম্বর ৪০, ৪০, ৫০, ৯০, ১০০। এদের গড় নম্বর ৬৪। কিন্তু এ নম্বরের সাথে বাস্তবতার মিল নেই। এসব ক্ষেত্রে মধ্যক ব্যবহার করা হয়। মধ্যক হলো সংগৃহীত উপাত্তের মধ্যম মান। যেমন, প্রদত্ত উপাত্তগুলোর মধ্যক হলো ৫০। প্রদত্ত উপাত্তসমূহ মানের ক্রমানুসারে (ঊর্ধ্বক্রম বা অধঃক্রম) সাজালে যে মান উপাত্তগুলোকে সমান দুইভাগে ভাগ করে তাকে মধ্যক বলে। যেমন, ১০, ৯, ১২, ৬, ১৫, ৭, ৮, ১৪, ১৩ সংখ্যাগুলোর মধ্যক কত? এখানে সংখ্যাগুলোকে মানের
ক্রমানুসারে সাজালে আমরা পাই,
| ৬, ৭, ৮, ৯ | ১০ | ১২, ১৩, ১৪, ১৫ |
লক্ষ করলে দেখা যায়, এখানে মোট ৯টি সংখ্যা আছে। এদের মধ্যক ১০ যা ক্রমানুসারে সাজানোর ৫তম পদ।
অর্থাৎ, মধ্যক তম পদ বা ৫তম পদ।
∴ মধ্যক = সংখ্যাগুলোর সংখ্যা + ১/২ , যদি উপাত্তের সংখ্যা বিজোড় হয়।
সুতরাং উপাত্তের সংখ্যা যদি বিজোড় হয়, তবে মধ্যক হবে ক্রমানুসারে সাজানোর মধ্যম পদ।
এখন, প্রশ্ন হচ্ছে উপাত্তের সংখ্যা যদি জোড় হয় তবে মধ্যক কী হবে? নিচের উদাহরণ লক্ষ করি:
৬,৪,৭,৮,৫,১২,১০,১১,১৪,১৫ সংখ্যাগুলোর মধ্যক নির্ণয়ের জন্য মানের ক্রমানুসারে সাজালে আমরা পাই ৪,৫,৬,৭,৮,১০,১১,১২,১৪,১৫। এক্ষেত্রে সংখ্যাগুলোকে সমান দুইভাগ করলে আমরা পাই,

প্রত্যেক ভাগে ৫টি করে সংখ্যা আছে। সুতরাং মধ্যক কত? মধ্যক নির্ণয় করতে হলে আমরা নিচের নিয়মে দুইভাগ করে থাকি:
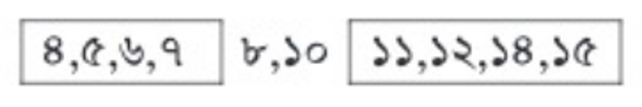
এখানে মধ্যক হবে ৮ ও ১০ এর গড়।
এখানে, সংখ্যাগুলোর সংখ্যা ১০ যা জোড় সংখ্যা এবং ৫ম ও ৬ষ্ঠ পদের বামে ও ডানে পদগুলোর সংখ্যা সমান।
সুতরাং, মধ্যক = ৫ম ও ৬ষ্ঠ পদের যোগফল/২
∴ মধ্যক =
| কাজ: ১ । তোমাদের শ্রেণির ১১ জন করে নিয়ে দল গঠন কর। নিজ নিজ দলের সদস্যদের বাংলা বিষয়ে শ্রেণি পরীক্ষায় প্রাপ্ত নম্বরের মধ্যক নির্ণয় কর। ২ । ১২ জন করে নিয়ে দল কর এবং দলের সদস্যদের উচ্চতা মেপে প্রাপ্ত উপাত্তের মধ্যক নির্ণয় কর। |
# বহুনির্বাচনী প্রশ্ন
১০ জন শিক্ষার্থীর ২০ নম্বরের পরীক্ষায় প্রাপ্ত নম্বরসমূহ নিম্নরূপ :
১১, ১২, ১৩, ১৫, ১৭, ১৮, ১৪, ১৮, ১৩, ১৮
১০ জন শিক্ষার্থীর গণিতে প্রাপ্ত নম্বর হলো:
৮৫, ৮০, ৯৫, ৯০, ৯৫, ৮৭, ৯৫, ৯০, ৯৫ ও ১০০।
উপাত্তগুলো লক্ষ কর: ৬, ৭, ৫, ৮, ১২, ১০, ১১, ৯, ১৩।
কোনো বিদ্যালয়ের ৬ষ্ঠ শ্রেণির ১০ জন শিক্ষার্থীর গণিতে প্রাপ্ত নম্বর:
৮৫,৮০,৯৫,৯০,৯৫,৮৭,৯৫,৯০,৯৫,১০০
সংখ্যাগুলোকে মানের ঊর্ধ্বক্রমে সাজালে আমরা পাই, ৮০,৮৫,৮৭,৯০,৯০,৯৫,৯৫,৯৫,৯৫,১০০।
এখানে, ৯০ আছে ২ বার, ৯৫ আছে ৪ বার এবং বাকি নম্বরগুলো আছে ১ বার করে। ৯৫ আছে সর্বাধিক বার। ৯৫ কে প্রদত্ত উপাত্তগুলোর প্রচুরক বলে। সুতরাং প্রচুরক হলো প্রদত্ত উপাত্তের মধ্যে যে সংখ্যা বা সংখ্যাগুলো সর্বাধিক বার থাকে।
আবার ৩,৬,৮,১,৯ সংখ্যাগুলোর মধ্যে কোনো সংখ্যা এক বারের বেশি না থাকায় এখানে প্রচুরক নেই।
উদাহরণ ৪। কোনো বিদ্যালয়ের ৬ষ্ঠ শ্রেণির ২০ জন ছাত্রের ইংরেজি বিষয়ে প্রাপ্ত নম্বর নিচে দেওয়া হলো। এদের প্রচুরক নির্ণয় কর।
৭৫,৬০,৭১,৬০,৮০,৭৮,৯০,৭৫,৮০,৯২,৮০,৯০,৯৫,৯০,৮৫,৯০,৭৮,৭৫,৯০,৮৫।
সমাধান: উপাত্তগুলোকে মানের ঊর্ধ্বক্রমে সাজানো হলো:
৬০,৬০,৭১,৭৫,৭৫,৭৫,৭৮,৭৮,৮০,৮০,৮০, ৮৫, ৮৫,৯০,৯০,৯০,৯০, ৯০, ৯২,৯৫।
এখানে, ৬০ আছে ২ বার, ৭৫ আছে ৩ বার, ৭৮ আছে ২ বার, ৮০ আছে ৩ বার, ৮৫ আছে ২ বার, ৯০ আছে ৫ বার এবং বাকি নম্বরগুলো আছে ১ বার করে। ৯০ সর্বাধিকবার আছে। সুতরাং নির্ণেয় প্রচুরক ৯০।
কাজ: ১। তোমাদের শ্রেণির সকলের উচ্চতা সেন্টিমিটারে মেপে ক্রমানুসারে সাজাও এবং উপাত্তগুলোর প্রচুরক নির্ণয় কর। |
# বহুনির্বাচনী প্রশ্ন
১০ জন শিক্ষার্থীর গণিত বিষয়ে প্রাপ্ত নম্বর নিম্নরূপ : ৭০, ৮০, ৯০, ৫০, ৮৫, ৮০, ৮৪, ৯০, ৮০, ৭৯
উপাত্তগুলো লক্ষ কর: ৬, ৭, ৫, ৮, ১২, ১০, ১১, ৯, ১৩।
তথ্য ও উপাত্ত সংক্রান্ত বিষয়াদি এবং তাদের গুরুত্ব ও দৈনন্দিন জীবনে ব্যবহার নিয়ে আলোচনা করা হয়েছে। উপাত্তসমূহের সারণিবদ্ধ করাও আলোচিত হয়েছে। এখন, উপাত্তসমূহের লেখচিত্র নিয়ে আলোচনা করা হবে। লেখচিত্রের মাধ্যমে উপাত্তসমূহের বহুল ব্যবহার আমরা দেখতে পাই। লেখচিত্রের মাধ্যমে যদি উপাত্তসমূহ উপস্থাপন করা হয়, তবে তা হয় চিত্তাকর্ষক ও বোঝার জন্য খুব সহজ। যেমন, ক্রিকেট খেলার প্রতি ওভারের রান সহজ উপায়ে দেখানোর জন্য স্তম্ভলেখের মাধ্যমে উপস্থাপন করতে দেখা যায়। এভাবে উপাত্তসমূহ বিভিন্ন প্রকার লেখচিত্রের মাধ্যমে উপস্থাপন করা - হয়। এখানে শুধুমাত্র রেখাচিত্র নিয়ে আলোচনা করা হবে।
উদাহরণ ৫। কোনো স্কুলে ষষ্ঠ শ্রেণিতে অধ্যয়নরত ৬ জন শিক্ষার্থীর উচ্চতা (সে.মি.তে) হলো:
১৪০, ১৪৫, ১৫০, ১৬০, ১৫০, ১৬৫।
এই উপাত্তের রেখাচিত্র আঁক।
সমাধান: ছক কাগজে পরস্পর লম্ব দুইটি সরলরেখা আঁকা হলো। আমরা জানি, অনুভূমিক রেখা x-অক্ষ এবং x-অক্ষের উপর লম্ব সরলরেখা y-অক্ষ যারা 0 বিন্দুতে ছেদ করেছে। এখন x-অক্ষের দুই ঘর পরপর একটি বিন্দুকে শিক্ষার্থী ধরে এবং y-অক্ষের প্রতি ঘরকে উচ্চতার একক ধরে রেখাচিত্রটি আঁকা হয়েছে। যেহেতু y-অক্ষ বরাবর ১৪০ থেকে আরম্ভ করা হয়েছে সেহেতু y-অক্ষের মূল বিন্দুর উপরে একটি ভাঙা চিহ্ন নিয়ে বোঝানো হয়েছে যে ০ থেকে ১৪০ পর্যন্ত ঘরগুলো আছে।

উদাহরণ ৬। তন্দ্রা চাকমা হাসপাতালে ভর্তি হয়েছে। ৩ ঘণ্টা অন্তর ১ দিনের তাপমাত্রা নিচের রেখাচিত্রের সাহায্যে দেখানো হয়েছে। এই রেখাচিত্র থেকে আমরা কী বুঝি?

সমাধান: ছক কাগজে x-অক্ষ বরাবর সময় এবং y-অক্ষ বরাবর তাপমাত্রা ধরা হয়েছে। ছক কাগজের ৫ ঘর পরপর দুপুর ১২টা থেকে রাত ১২টা পর্যন্ত ৩ ঘণ্টা অন্তর সময় এবং y-অক্ষ বরাবর প্রতি ঘরকে একক ধরে তাপমাত্রা দেখানো হলো। সময় অনুযায়ী ছক কাগজে তাপমাত্রা বিন্দু দিয়ে চিহ্নিত করা হয়েছে। বিন্দুগুলোকে রেখাংশ দিয়ে সংযোগ করে তাপমাত্রার রেখাচিত্র আঁকা হলো।
প্রায় ৯৮°F পর্যন্ত মানুষের তাপমাত্রা স্বাভাবিক ধরা হয় বিধায় y-অক্ষ বরাবর নিচের তাপমাত্রাসমূহ উহ্য রাখা হয়েছে। তাপমাত্রার এই রেখাচিত্র থেকে প্রতীয়মান হয় যে, বেলা ৩.০০ টার তাপমাত্রা সর্বাধিক ১০২° হয়। রাত ৯.০০টা ও রাত ১২.০০ টায় তাপমাত্রা ১০০° তে স্থির থাকে।
উদাহরণ ৭। বাংলাদেশের ক্রিকেট টিমের কোনো এক খেলায় ওভারপ্রতি রান নিচের সারণিতে দেওয়া হলো :
| ওভার | ১ম | ২য় | ৩য় | ৪র্থ | ৫ম | ৬ষ্ঠ | ৭ম | ৮ম | ৯ম | ১০ম |
| রান | ৮ | ১০ | ৬ | ৫ | ০ | ৮ | ৬ | ৪ | ৭ | ১২ |
ক. ওভারপ্রতি সর্বোচ্চ এবং সর্বনিম্ন রানের পার্থক্য নির্ণয় কর।
খ. ওভার প্রতি রানকে ক্রম অনুসারে সাজিয়ে রানের গড় নির্ণয় কর।
গ. প্রদত্ত তথ্যের রেখাচিত্র অঙ্কন কর।
সমাধান:
(ক) সর্বোচ্চ রান ১২
এবং সর্বনিম্ন রান ০
সর্বোচ্চ এবং সর্বনিম্ন রানের পার্থক্য (১২-০) = ১২
(খ) ওভারপ্রতি রানকে ঊর্ধ্বক্রমে সাজিয়ে পাই ০, ৪, ৫, ৬, ৬, ৭, ৮, ৮, ১০, ১২
রানের যোগফল = ০+৪+৫+৬+৬+৭+৮+৮+১০+১২
= ৬৬ রান
∴ ওভারপ্রতি রানের গড় = মোট রান/মোট ওভার
= ৬.৬
(গ) ছক কাগজে পরস্পর লম্বা দুইটি সরলরেখা আঁকা হলো। অনুভূমিক রেখা X অক্ষ বরাবর এবং X অক্ষের উপর লম্ব সরলরেখা Y অক্ষ বিন্দুতে ছেদ করেছে। এখন X অক্ষের প্রতি পাঁচ ঘর পরপর একটি বিন্দুকে ওভার এবং Y অক্ষের প্রতি দুই ঘর পরপর একটি বিন্দুকে রান ধরে রেখাচিত্রটি আঁকা হয়েছে।

| কাজ: উদাহরণ ৭ এর আলোকে একটি সমস্যা তৈরি কর এবং সমাধান কর। |
সঠিক উত্তরে টিক (√) চিহ্ন দাও:
১। ৪, ৬, ৭, ৯,১২ সংখ্যাগুলোর কোনটি মধ্যক?
(ক) ৭
(খ) ৬
(গ) ৯
(ঘ) ১২
২। ৮, ৯, ১০, ১২, ১৪, ১৬ সংখ্যাগুলোর কোনটি মধ্যক?
(ক) ৯
(খ) ১১
(গ) ১৬
(ঘ) ১৪
৩। ৪,৫,৮,৬,৭,১২ সংখ্যাগুলোর কোনটি প্রচুরক?
(ক) ৬
(খ) ৭
(গ)১২
(ঘ) প্রচুরক নেই
৪। ৮, ১২, ১১, ১২, ১৪, ১৮ সংখ্যাগুলোর কোনটি প্রচুরক?
(ক) ৮
(খ) ১১
(গ) ১২
(ঘ) ১৮
৫। উপাত্তের সংখ্যা জোড় হলে মধ্যক নিচের কোনটি?
(ক) মধ্য পদদ্বয়ের গড়
(খ) মধ্য পদদ্বয়ের সমষ্টি
(গ) শেষ পদদ্বয়ের গড়
(ঘ) প্রথম দুইটি পদের সমষ্টি
৬। ৪৮, ২২, ২৮, ২৫, ১৫ উপাত্তগুলো কোন ধরনের?
(ক) বিন্যস্ত
(খ) অবিন্যস্ত
(গ) ঊর্ধ্বক্রমে সাজানো
(ঘ) অধঃক্রমে সাজানো
৭। নিচের কোন উপাত্তগুলো বিন্যস্ত?
(ক) ৮, ৬, ০, ৪
(খ) ২, ৪, ২, ৪
(গ) ৮, ৬, ৪, ২
(ঘ) ২, ৪, ৮, ০
৮। ৬, ১২, ২২, ২২, ২৬, ৩০, ৩৬ উপাত্তসমূহের?
(i) প্রচুরক ২২
(ii) মধ্যক ২২
(iii) গড়, মধ্যক ও প্রচুরক পরষ্পর সমান
নিচের কোনটি সঠিক?
(ক) i ও ii
(খ) i ও iii
(গ) ii ও iii
(ঘ) i, ii, ও iii
নিচের তথ্যের আলোকে ৯-১২ নং প্রশ্নের উত্তর দাও:
৬ জন শিক্ষার্থীর ২০ নম্বরের পরীক্ষায় প্রাপ্ত ফলাফল:
৮, ১০, ১৬, ১৪, ১৬, ২০
৯। উপাত্তসমূহের প্রচুরক কত?
(ক) ৮
(খ) ১৪
(গ) ১৬
(ঘ) ২০
১০। মধ্যক কত?
(ক) ১৪
(খ) ১৫
(গ) ১৬
(ঘ) ৩০
১১। গড় কত?
(ক) ১৩.৬
(খ) ১৪
(গ) ১৬
(ঘ) ১৬.৮
১২। উপাত্তগুলোর সঠিক তথ্য হলো-
(i) সর্বোচ্চ নম্বর ১৬
(ii) সর্বোচ্চ ও সর্বনিম্ন নম্বরের পার্থক্য ১২
(iii) পরীক্ষায় প্রাপ্ত সর্বনিম্ন নম্বর ৪০%
নিচের কোনটি সঠিক?
(ক) i ও ii
(খ) i ও iii
(গ) ii ও iii
(ঘ) i, ii, ও iii
১৩ । তথ্য ও উপাত্ত কী? উদাহরণের মাধ্যমে উপস্থাপন কর।
১৪। কালামের ওজন ৫০ কেজি। আবার ৬ষ্ঠ শ্রেণির শিক্ষার্থীদের গড় ওজন ৫০ কেজি। এই দুই তথ্যের কোনটি দ্বারা পরিসংখ্যান বোঝায়? ব্যাখ্যা কর।
১৫। তোমাদের শ্রেণির ২০ জন ছাত্র-ছাত্রীর গণিতে প্রাপ্ত নম্বর ৩০,৪০,৩৫,৫০,৬০,৭০, ৬৫,৭৫,৬০,৭০,৬০,৩০,৪০,৮০,৭৫,৯০,১০০,৯৫,৯০,৮৫।
(ক) এই উপাত্তগুলো কি বিন্যস্ত উপাত্ত?
(খ) উপাত্তগুলো অবিন্যস্ত হলে বিন্যস্ত কর।
(গ) উপাত্তগুলোকে মানের ঊর্ধ্বক্রম ও অধঃক্রম অনুসারে সাজাও।
১৬। তোমার শ্রেণির ১৫ জনের ওজন উপস্থাপন কর এবং গড় নির্ণয় কর।
১৭। নিম্নলিখিত উপাত্তগুলোর মানের মধ্যক নির্ণয় কর।
৯, ১২, ১০, ৬, ১৫, ৮, ৭, ১৪, ১৩।
১৮। নিম্নলিখিত উপাত্তসমূহের মধ্যক নির্ণয় কর:
১৪০০, ২৫০০, ১৫০০, ৭০০, ৬০০, ৯০০, ১০৫০, ১১০০, ৮০০, ১২০০।
১৯। ৯, ১৬, ১৪, ২২, ১৭, ২০, ১১, ৭, ১৯, ১২, ২১ উপাত্তসমূহের মধ্যক নির্ণয় কর।
২০। ৫, ৭, ১২, ১০, ৯, ১৯, ১৩, ১৫, ১৬, ২৪, ২১, ২৩, ২৫, ১১, ১৪, ২০ সংখ্যাগুলোর মধ্যক নির্ণয় কর।
২১। কোনো উপাত্তের সাংখ্যিক মান ৪,৫,৬,৭,৮,৮,৯,১১,১২। এদের প্রচুরক নির্ণয় কর।
২২। ৩, ৪, ৬, ৭, ৮, ৯, ১০, ১১ সাংখিক মানের উপাত্তসমূহের প্রচুরক নির্ণয় কর।
২৩। নিচে ৩৮ জন শ্রমিকের সাপ্তাহিক সঞ্চয় (টাকায়) দেওয়া হলো,
১৫৫,১৬৫,১৭৩,১৪৩,১৬৮, ১৪৬,১৫৬,১৬২,১৫৮,১৪৮,১৫৯,১৪৭,১৫০,১৩৬,১৩২,১৫৬,১৪০, ১৫৫,১৪৫,১৩৫,১৫১,১৪১,১৬৯,১৪০,১২৫,১২২,১৪০,১৩৭,১৪৫,১৫০,১৬৪,১৪২,১৫৬, ১৫২, ১৪৬,১৪৮,১৫৭ ও ১৬৭।
(ক) মানের ক্রমানুসারে উপাত্তসমূহ সাজাও, সারণিবদ্ধ কর ও গড় নির্ণয় কর।
(খ) উপাত্তসমূহের মধ্যক ও প্রচুরক নির্ণয় কর।
২৪। সকাল ৬.০০ থেকে শুরু করে সুজনের ৩ ঘণ্টা অন্তর ১২ ঘণ্টার তাপমাত্রা (ফারেনহাইট) রেখাচিত্রের মাধ্যমে দেখাও:
(ক) ০° থেকে ৯৮° পর্যন্ত তাপমাত্রা অক্ষ থেকে কেন বাদ দেওয়া হয়েছে?
(খ) ১২ ঘণ্টায় তাপমাত্রার প্রকৃতি সম্বন্ধে বর্ণনা দাও।
২৫। একজন শিক্ষার্থী ২০ থেকে ৪০ পর্যন্ত সংখ্যাগুলোর মধ্যে নিম্নের সংখ্যাগুলো লিখল।
২১,৩৭,৪০,২২,৩৯,৩৫, ২২,২৫,৩২,২২,২১,৩৭,৪০,২২,৩৯,৩৫,২৫,৩২,২২,৩৭,৩৯,৩২,২২,৩৭,
৩২,৪০,৩৭,২২,৩৫,২২.
(ক) প্রদত্ত সংখ্যাগুলোকে মানের ক্রম অনুসারে সাজিয়ে লেখ।
(ক) উপাত্তগুলোর মধ্যক ও প্রচুরক নির্ণয় কর।
(গ) প্রদত্ত তথ্য উপাত্তের রেখাচিত্র অঙ্কন কর।






